Convex Functions
Recall that a function \(f:I\to \mathbb R\) is called convex if \[ f(tx+(1-t)y)\le tf(x)+(1-t)f(y) \] for any \(t\in[0,1]\) and \(x,y\in I\) where \(I\) is an interval in \(\mathbb R\). In some context, \(f\) is called \(p\)-convex if \(f^p\) is convex in the meaning of (1). \(f\) is called quasi-convex if \[ f(t)\le\max\{f(a),f(b)\} \] for any \(t\in [a,b]\). Note that if \(f\) is convex then \(f\) is necessarily quasi-convex. Quasi-convex functions are also called peakless in Busemann's articles.
If \(f\) is differentiable, then we have a simple rule to determine its convexity: \(f\) is convex if and only if \(f'\) is non-decreasing. If \(f\) is twice differentiable, then \(f\) is convex if and only if \(f''\) is non-negative. From these rules we can see that convexity is a local property for differentiable functions. i.e. say that \(f\) is locally convex if for any \(x\) there is a neighborhood such that \(f\) is convex on that neighborhood. If \(f\) is differentiable and locally convex, by the above discussions locally convexity implies global convexity.
The question is whether, without the presuppose of differentiability, local convexity implies global convexity. i.e if \(f\) is defined on an interval such that any point has a neighborhood where condition (1) holds, is \(f\) convex or not? Recall the following sufficient and necessary condition for \(f\) being convex: \(f\) is convex if and only if its epigraph is convex, where the epigraph of \(f\) is defined by \[ epi(f)=\{(t,y)|y\ge f(t)\} \] We see that local convexity is equivalent to that each point in the epigraph has a neighborhood which is convex. Thus we come to the question: Let \(X\) be a locally convex set in \(\mathbb R^n\), is itself convex?
Tietze-Nakajima Theorem
The above question is answered by the classical Tietze-Nakajima theorem.
Let \(X\) be a closed subset in \(\mathbb R^n\). \(X\) is convex if and only if \(X\) is connected and locally convex.
Necessity is clear since convexity implies connectedness and local convexity. Note that local convexity implies local path connectedness. Thus \(X\) being connected is equivalent to \(X\) being path connected. We can define a length structure on \(X\) by defining admissible paths to be polygonal paths (the existence of polygonal paths is guaranteed by local convexity) and length to be the canonical length in Euclidean spaces. The induced metric on \(X\) is midpoint convex (a special case of Menger convex). i.e. For any two point in \(X\) there exists a midpoint (The existence of midpoint relies on the closeness and local convexity of \(X\)). Since \(X\) is complete, by a theorem of BBI, \(X\) is strictly intrinsic. i.e. the induced metric coincides with the usual Euclidean metric and there is a shortest path, which is clearly a straight line, connecting any two point. Therefore \(X\) is convex.
Tietze-Nakajima theorem implies that the convexity of functions is a local property. In contrast, quasi-convexity is not a local property. i.e if a function is local quasi-convex, it may not be a quasi-convex function globally. For a counterexample, consider the exterior of '风'.
From the proof we see that the local-to-global convexity property for Euclidean spaces should have a natural generalization to distance geometry. However, one should be careful with the notion of 'convexity' and the choice of 'proper' spaces. See a series of questions discussed in StackExchange (Does convexity implies contractibility in length space?; Is a uniquely geodesic space contractible? I; On continuously uniquely geodesic space; Are small \(\epsilon\)-balls convex in geodesic metric spaces?)
Generalized Hadamard-Cartan Theorem
M. Gromov stated a theorem which generalized the classical Hadamard-Cartan theorem in Riemannian geometry:
A simply-connected, complete, locally convex geodesic space is globally convex; hence any two points are joined by a unique geodesic.
A geodesic space is a space where any two points can be joined by a shortest path. A subset \(A\) is convex if for any two scaled geodesics \(\alpha,\beta:[0,1]\to A\) the function \(d(\alpha(t),\beta(t))\) is convex. If \(m_{pq}\) denotes the midpoint of a geodesic from \(p\) to \(q\). Then convexity is equivalent to \(2d(m_{pq},m_{pr})\le d(q,r)\) for any three distinct points. Thus the generalized Hadamard-Cartan theorem shows that local-to-global convexity holds for simply-connected, complete, geodesic spaces. A detailed proof of this theorem is given by S. Alexander and R. Bishop in 1990.
Let \(m\in X\) be a fixed point in the geodesic space. Let \(\mathbb G_m\) be the space of geodesics starting at \(m\), carrying the uniform distance \(\mathbf d\). \(m\) has no conjugate points if the endpoint map \[ EP:\mathbb G_m\to X \] defined by \(EP(\gamma)=\gamma(1)\), is a local homeomorphism. i.e. \(EP\) maps a neighborhood of each \(\gamma\) homeomorphically onto a neighborhood of \(\gamma(1)\). That is to say, each point has a neighborhood such that the geodesics vary continuously. The first theorem shown by AB is that
A locally convex, complete geodesic space has no conjugate point.
Using local convexity, it is easy to prove that \(EP\) is an isometry on a neighborhood of \(\gamma\) onto its image. The question is that whether this image is a neighborhood of \(\gamma(1)\). AB proved that, in fact, \(EP\) is an isomorphism from a ball of \(\gamma\) to a ball of \(\gamma(1)\) by using an induction method.
\(X\) is said to have neighborhoods of bipoint uniqueness if there are neighborhoods such that any two points of which is joined by a unique shortest geodesic varying continuously with its endpoints. If \(X\) is locally convex, then \(X\) has neighborhoods of bipoint uniqueness by the following argument.
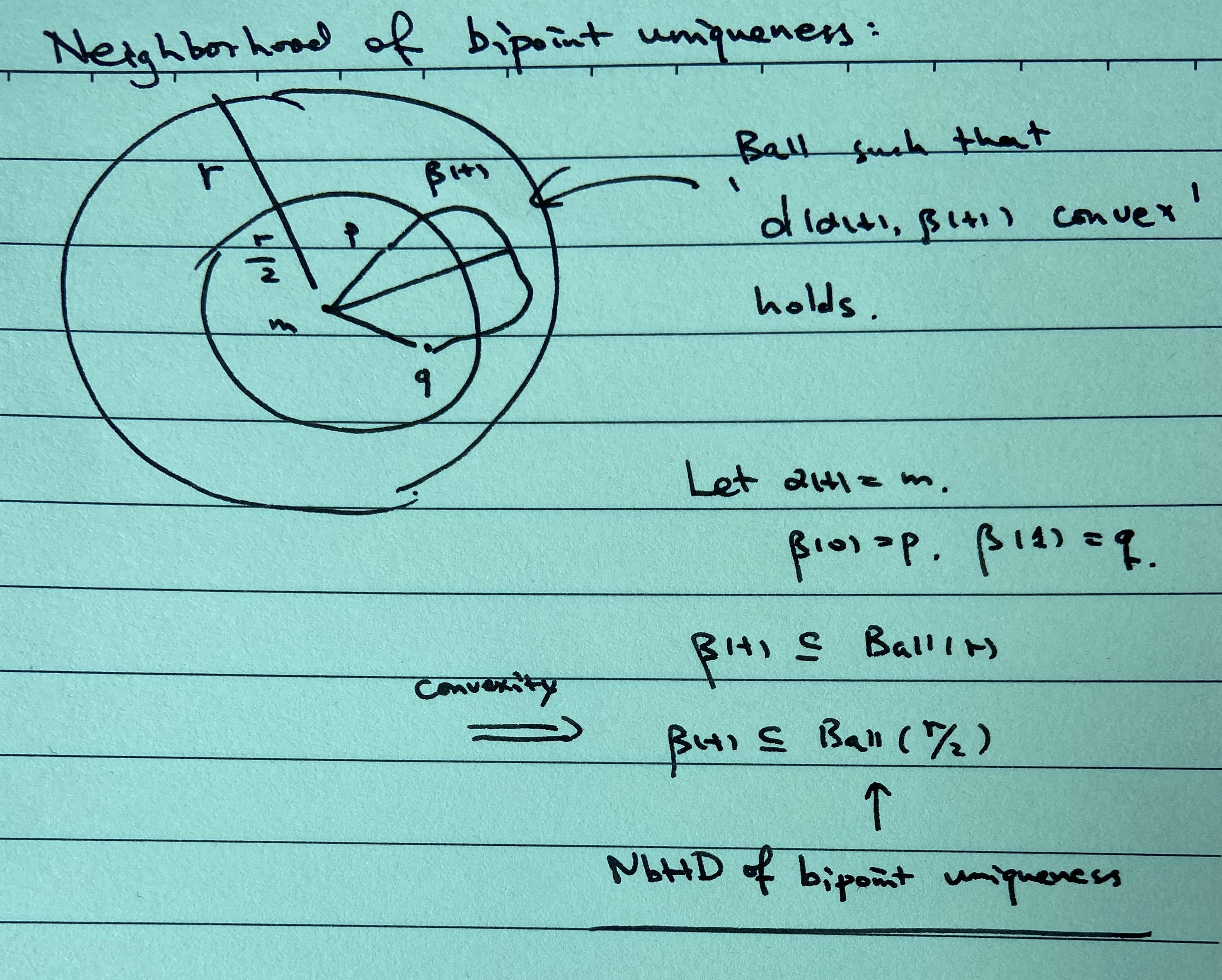
The following lemma says \(EP\) is a covering map
Let \(\phi:\overline{M}\to M\) be a local isometry. \(\overline{M}\) and \(M\) are complete intrinsic metric spaces and \(M\) has neighborhoods of bipoint uniqueness. Then \(\phi\) is a covering map.
Since \(\mathbb G_m\) is contractible thus connected and simply connected, it suffices to define a complete intrinsic metric \(\bar{\mathbf d}\) on \(\mathbb G_m\) so that \((\mathbb G_m,\bar{\mathbf d})\) is complete and \(EP\) is local isometry. One verifies that the metric induced by \(\mathbf d\) is exactly \(\bar{\mathbf d}\).
CAT(\(\kappa\)) Spaces
CAT\((\kappa)\) spaces are spaces with curvature bounded above in the Alexandrov sense. Let \(x,y,z\) be distinct points in a length space \(X\) and call \(\Delta xyz\) a geodesic triangle if the segments \(xy,yz,zx\) are geodesics. For any \(\kappa\in\mathbb R\), the comparison space of curvature \(\kappa\) is the unique simply-connected Riemannian 2-manifold of constant sectional curvature \(\kappa\), denoted by \(M_\kappa\). Define the diameter of \(M_\kappa\) as \[ D_\kappa=\left\{\begin{array}{l}\infty, \kappa\le 0\\ \pi/\sqrt{\kappa},\kappa>0\end{array}\right. \] For a \(D_\kappa\)-geodesic space \(X\) (i.e. points within distance \(D_\kappa\) are joined by a unique geodesic), a geodesic triangle \(\Delta\) is said to satisfy the CAT\((\kappa)\) inequality if there exists an expanding map \(f:\Delta\to M_\kappa\) such that \(f|_{\partial\Delta}\) is an isometry. Then \(X\) is called a CAT\((\kappa)\) space if every geodesic triangle with perimeter less than \(2D_\kappa\) satisfies the CAT\((\kappa)\) inequality.
A subset \(A\) in the CAT\((\kappa)\) space \(X\) is called convex if for any two points \(x,y\in A\) within distance \(D_\kappa\), the unique geodesic joining \(x,y\) is contained in \(A\). One easily verifies that these generalize the convexity in Euclidean spaces.
This paper shows that local-to-global convexity holds for all CAT\((\kappa)\) spaces. Specifically, the following theorem holds
Let \(A\subset X\) be a closed, connected, locally convex subset in CAT\((\kappa)\) space. Denote with \(l\) the induced length metric in \(A\). Then if \(diam_l(A)\le D_\kappa\), \(l\) coincides with the original length distance and \(A\) is convex.