Motivation
Let \(A\) stand for the true symmetric matrix and \(E\) represent the perturbation. Let \(\lambda_i\)'s be the eigenvalues of \(A\), sorted in descending order and denote \(\delta=\lambda_1-\lambda_2\) to be the eigengap. Let \(u_i\) be the eigenvector of \(A\) and \(v_i\) be the eigenvector of \(A+E\). The classical Davis-Kahan theorem states that
\[ \sin(u_1,v_1)\le \frac{2\|E\|_{op}}{\delta} \]
up to constant the DK bound is sharp, as we see in the following example
\[ A=\left[\begin{array}{cc} 1+\epsilon & 0\\ 0 &1-\epsilon \end{array}\right],\, E=\left[\begin{array}{cc} -\epsilon & \epsilon \\ \epsilon & \epsilon \end{array}\right] \]
However, researchers find that in certain cases the bound can be improved. In Vu's paper, the author considered the following setting: \(A\) is an \(n\times n\) matrix but of low rank \(r\), \(E\) is a random Bernoulli matrix whose entries are iid random variables taking values \(\pm 1\) with probability \(1/2\). From random matrix theory we know that \(\|E\|_{op}=(2+o(1))\sqrt{n}\). Then the classical DK bound is about \(4\sqrt{n}/\delta\). But the experiment shows that this bound is far from optimal.
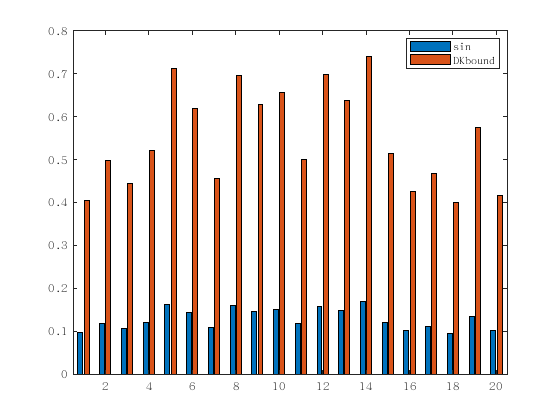
In the experiment we construct a \(400\times 400\) matrix \(A\) such that \(A(1,1)=10+\delta, A(2,2)=10\) and zero otherwise. We set \(\delta=100(1+rand)\) where \(rand\) is uniform on \([0,1]\) and we run 20 times. The blue bar represents the true \(\sin\) and red bar represents the classical DK bound. The result motivates us to find a sharper bound in random settings.
Random Noises
We state a simplified assumption on the random matrix \(E\) from Vu (just omit the constants). The \(n\times n\) matrix \(E\) is \(\gamma\)-concentrated if for all unit vectors \(u,v\) and every \(t\) we have
\[ \log\mathbb{P}(|u^TEv|>t)=O(-t^\gamma) \]
i.e. the rate tending to \(-\infty\) is in order at least \(\gamma\).
Examples:
- Bernoulli matrix is \(2\)-concentrated;
- Gaussian matrix is \(2\)-concentrated;
- Sub-exponential matrix is \(1\)-concentrated.
In particular, for bounded random matrices we have
Let \(E=(\xi_{ij})\) be a matrix with independent random variables each with mean zero. Furthermore, \(|\xi_{ij}|\le K\) a.s. for all \(i,j\). Then \(E\) is \(2\)-concentrated and \[ \mathbb{P}(|u^TEv|>t)\le 2\exp(\frac{-t^2}{2K^2}) \]
Improved DK bound
Note that
\[ \sin^2\angle (u_1,v_1) = 1-\cos^2\angle (u_1,v_1) = \sum_{i=2}^n |u_k\cdot v_1|^2 \]
Thus it suffices to bound \(|u_k\cdot v_1|\). In fact, Let \(Q=[u_2,\cdots,u_r]\) and \(P=[u_{r+1},\cdots,u_n]\). we want to bound
\[ \|Q^Tv_1\|^2 \text{ and } \|P^Tv_1\|^2 \]
For \(Q^Tv_1\) we have
\[ Q^T(A+E)v_1-Q^TAv_1=Q^TEv_1 \]
which is equivalent to
\[ (\mu_1I-\Lambda_r)Q^Tv_1 = Q^TEv_1 \]
where \(\Lambda_k\) is the diagonal matrix consisting of \(\lambda_2,\cdots,\lambda_r\). It follows
\[ |\mu_1-\lambda_2|\|Q^Tv_1\|\le \|Q^TEv_1\| \]
Thus we need a lower bound for gap \(|\mu_1-\lambda_2|\) and an upper bound for \(|Q^TEv_1|\). For \(\mu_1\) we have
\[ \mu_1 = \|A+E\|_{op}\ge u_1^T(A+E)u_1 = \lambda_1 + u_1^TEu_1 \]
Since \(E\) is \(\gamma\)-concentrated, we see that \(\mu_1\ge \lambda_1-t\) with probability at least \(1-\exp(O(-t^\gamma))\). If the eigengap \(\delta=\lambda_1-\lambda_2\) is sufficient large (for example, \(\delta= 2t\)) then \(\mu_1-\lambda_2>\delta/2\) with probability at least \(1-\exp(O(-\delta^\gamma))\).
From the above discussion we know \(\mu_1\ge \lambda_1/2\) with probability at least \(1-\exp(O(-\lambda_1^\gamma))\). Then
\[ (PP^Tv_1)^T(A+E)v_1-(PP^Tv_1)^TAv_1=(PP^Tv_1)^TEv_1 \]
Note that \(P^TA=0\) by our construction and so \(\mu_1(PP^Tv_1)^Tv_1=(PP^Tv_1)^TEv_1\). We know that
\[ \|P^Tv_1\|^2 = (PP^Tv_1)^Tv_1 \le \frac{1}{\mu_1}\|P^Tv_1\|\|E\|_{op} \]
Therefore, \(\|P^Tv_1\|\le 2\|E\|_{op}/\lambda_1\) with probability at least \(1-\exp(O(-\lambda_1^\gamma))\).
Now if we write \(v_1= (I-PP^T)v_1+PP^Tv_1\) then
\[ \|Q^TEv_1\|\le \|(I-PP^T)^TE(I-PP^T)\|_{op}+\|E\|_{op}\|P^Tv_1\| \]
By a standard \(\epsilon\)-net argument the first term is proved to be no greater than \(tr^{1/\gamma}\) with probability at least \(1-\exp(O(-rt^\gamma)+O(r))\). Above all we have
\[ \|Q^Tv_1\|\le \frac{2}{\delta}(tr^{1/\gamma}+2\frac{\|E\|_{op}^2}{\lambda_1}) \]
with probability at least \(1-\exp(O(-rt^\gamma)+O(r))-\exp(O(-\lambda_1^\gamma))-\exp(O(-\delta^\gamma))\).
Finally we see that the new bound is related to three items: the largest eigenvalue \(\lambda_1\), the eigengap \(\delta\) and the rank \(r\):
\[ \sin\angle (u_1,v_1)\le 4(\frac{tr^{1/\gamma}}{\delta}+\frac{\|E\|_{op}}{\lambda_1}+\frac{\|E\|^2_{op}}{\lambda_1\delta}) \]
with probability at least \(1-\exp(O(-rt^\gamma)+O(r))-\exp(O(-\lambda_1^\gamma))-\exp(O(-\delta^\gamma))\).
Remark 1. This result is only nontrivial if the amplitude of \(\lambda_1\) is much larger than \(\delta\) and \(\|E\|_{op}\) (otherwise when \(\lambda_1\sim\delta\) the bound is worse than classical DK bound). In this case the bound is \(O(r^{\gamma}/\delta)\) which is much better than \(O(n^{1/\gamma}/\delta)\).
Remark 2. From the above simulation we see that the bound is not sharp. Therefore there are chances to obtain better results for random perturbations.